| Adapted for the Internet from: Why God Doesn't Exist |
| A mathematician defines perpendicular with numbers |
- 1.0 In Mathematics, the definition of perpendicular requires numbers
Euclid was among the first to define geometric figures formally. He defined perpendicular as follows:
- “ When a straight line standing on a straight line makes the adjacent angles equal
to one another, each of the equal angles is right, and the straight line standing
on the other is called a perpendicular to that on which it stands.” (Bk. I, Def. 10) [1]
Euclid's definition has been carried over in different ways by his successors:
- “ Two lines, vectors, planes, etc., are said to be perpendicular if they meet at a
right angle.” [2]
“ two vectors are said to be perpendicular to one another if Q(ab) = 0.” (p. 29) [3]
This means that, under the mathematical notions, if the ET wants to understand what two perpendicular
lines are on our planet, he needs to attend high school or college and learn trig! The ET first needs to
understand what an angle is and then, specifically, what a 90° angle is.
Do you need to learn Math to visualize two perpendicular lines?If I point to an ideal cross, would you
recognize the components as lying perpendicular to each other without knowing what a 90° angle is?
2.0 A point can’t be perpendicular to anything
A mathematician begins his presentation alleging that a point may run perpendicular to something else:
- “ a point and a line, which is normal (perpendicular) to the plane” [4]
Actually, a point can’t be perpendicular to anything if it has no extension. You must stretch the point
retroactively on your own:
- “ Only one perpendicular may be drawn from a point to a straight line, or through
a point on the line." (p. 149) [5]
This means that you must amend the definition of point to certify that it is perpendicular. Perhaps the
mathematicians can argue that the line we extend to the point is perpendicular, but not the point itself.
The mathematicians read too much into their exhibits.
3.0 The mathematical point doesn't have shape
But there is a more fundamental problem. Euclid hasn’t defined the shape of his point, remember? For
example, if his point is spherical, even under the relativistic version of angle, a series of round points
won't form the required two straight lines (Fig. 1 A). Yet more basic, if his points are conceptually just
abstract locations as opposed to 2-D or 3-D dots, we don't have a geometric line to begin with.
4.0 In Mathematics, an L is not a perpendicular
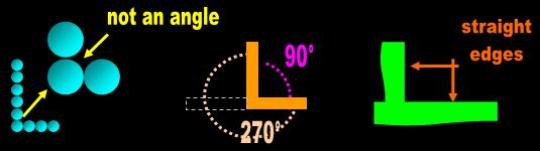
Another problem the mathematical definition causes is that it eliminates figures that have the shape of
the letter 'L'. Euclid's definition only allows figures having the shape of a 'T'. In Mathematics, the two
angles on either side of the perpendicular (adjacent angles) must be equal (i.e., both must be 90°):
- “ perpendicular: either of two lines that form equal adjacent angles, or right
angles, with each other." (p. 149) [6]
- Unfortunately, an L has a 90° angle on one side and a 270° degree angle on the other (Fig. 1 B). The
adjacent angles are not equal.
The mathematicians get around this restriction artificially. What they do is cheat. They wave their magic
wand, stretch one of the lines comprising the L, and forcefully convert the L into an inverted T. What the
mathematicians do in effect is amend their definition of line segment retroactively. They forcefully
convert the line segment (finite) into a line (infinite) and proceed as if nothing happened. An L is not
made of lines. It is comprised of two line segments. By extending them, Euclid and his disciples have
unjustifiably altered their initial assumptions.
- 5.0 The perpendicular of Physics
In Physics, it is not nearly as complicated as all this. You should be able to look at two lines in the
horizon and call them perpendicular without taking any measurements or knowing for sure whether
they are or not. We are talking about defining the adjective perpendicular rather than about proving
whether two lines are perpendicular.
It turns out that, after all is said and done, we don’t even need lines to define perpendicular anyway.
What we need is two edges, one of which lies horizontally and the other stands vertically (Fig. 1 C). We
just need to define what we mean by horizontal and vertical. Horizontal, as the word indicates, means that
a straight edge or line lies parallel with the observer's horizon, a word which the Greeks used to refer to
the limit or boundary of the landscape the observer could see. The Sun rose and set on this horizon, and
so did the Moon, the planets, and the stars, forming the ever important ancient constellations. Vertical
comes from the Latin vertex, meaning 'highest point,' or verticalis, meaning 'overhead.' It is used as a
synonym of upright to contrast it with horizontal. Our forefathers noticed that the Sun was at its highest
point at noon. They also had to develop a vocabulary to refer to a celestial body hovering overhead.
Indeed, they didn't even need the horizon as a reference after they invented the plumb line, a tool they
used extensively to construct buildings. At least as early as the 3rd Dynasty, the Egyptians used
rudimentary tools such as plumb bobs and celestial objects to construct their magnificent pyramids.
Hence, there is no more mystery than this. A horizontal line is one that lies parallel with the horizon and
a vertical line hangs down from an overhead location like a plumb line pulled by gravity. We need no
knowledge of angles to understand any of these concepts. Perpendicular is not a term of Mathematics.
It is exclusively a qualitative notion.
The term that has come down to us from the ancients to refer to this pattern is perpendicular, a derivative
of 'perpendiculum', meaning 'plumb line.' As all our stupid mathematicians, Euclid overdid it a bit and
complicated himself unnecessarily by trying to give this pattern an mathematical description. Fortunately,
we can improve on his definition:
- perpendicular (adj.): 1. A pattern formed by two straight edges, one lying horizontally
and the other standing vertically. 2. A straight edge that hangs or runs like a
plumb line with the horizon as a backdrop.
Fig. 1 The perpendiculars of Mathematics and Physics |


Is that perpendicular
enough for you, boss?
enough for you, boss?
- Math
B. L-shaped angle (Is an L a perpendicular?)
- Phyz
| A |
| B |
| C |
- Module home page: A mathematician says that a rectilinear path is straight
- Pages in this module:
- 3. This page: A mathematician defines perpendicular with numbers
- ________________________________________________________________________________________
- Copyright © by Nila Gaede 2008
