1.0   Counting units versus measuring magnitudes

    The mechanics would probably reject the notion of a ‘fundamental particle.’ They would argue perhaps
    that they have yet to zero in on an elusive indivisible. They would add that my proposal is not very useful
    (at least for their self-serving purposes) and that it is best taken up in Philosophy, which in their view is the
     proper forum for the argument I raise here. The way they see it, whether there is a fundamental particle at
    the end of the yellow brick road is a trivial matter that doesn’t concern Physics because the discussion
    involves no Mathematics and it is currently beyond the experimental and measurement capabilities of
    accelerators. Physics, so the argument goes, deals with hypotheses that a relativist can test in the lab and
    put into numbers in a journal. Nevertheless, in their minds, it would be totally impractical to count the
    number of particles that make up a muon or to specify its mass in these terms. Despite that they routinely
    smash particles and analyze the debris, the particle mathematicians are more comfortable determining the
    mass of a muon through measurement (energy, speed, momentum, etc.). The job of a particle mathematician
    is not to count particles. His job is to classify them!

    If this is their argument, we need to begin at a more fundamental level. The mathematicians confuse
     hypotheses with theory and have totally misconstrued the scientific method. Whether a muon is
    comprised of subcomponents is a question of assumptions and not an issue of proof. The theory of
    Quantum Mechanics absolutely requires and ‘predicts’ one or several fundamental particles because
    there is logically no way for a mathematician to divide a physical entity and end up with nothing. The
    splitting of a physical object does not result in nothing. The splitting of one ‘something’ necessarily
    results in two ‘somethings.’ Always! This is a conceptual issue. It is not something we verify in the lab.
    Therefore, QM cannot avoid it. This religion invariably conduces to the notion of the tiniest indivisible.
    The idiots of Mathematical Physics want you to believe that this is a philosophical issue, meaning a
    matter of opinion. It is not. Every mechanic has no choice but to accept that the ‘fundamental particle’
    is the underlying assumption of contemporary QM as well as of Mathematical Physics. It follows that
    every hydrogen atom should have a countable number of such units at any point in time whether we
    know this number or not. And so should the ‘mass-less’ photon!

    And here again we see why our mathematicians aren’t interested in the quantity of matter definition.
    Mathematics deals exclusively with motion and not at all with architecture. Mathematicians aren’t
    interested in shape (objective criterion). They have developed the erroneous notion that measurement
    is a synonym of science:

    " when you can measure what you are speaking about and express it in numbers,
       you know something about it; but when you cannot measure it and when you
       cannot express it in numbers, your knowledge is a meager and unsatisfactory
       kind: it may be the beginning of knowledge, but you have scarcely, in your
       thoughts, advanced to the stage of science." (William Thomson, Lord Kelvin)  [1]

    The mathematicians are only interested in measurement (subjective criterion). That’s why mechanics
    and special relativists talk endlessly about the opinions each observer has in regards to the mass of a
    traveling object. They are attempting to resolve an objective issue using subjective tools. When the
    mathematicians use the word mass, they mean inertia, which is not at all the same as number of particles
    . Quantity of particles you count. Inertia you measure. Mathematicians determine mass by measuring
    resistance or force. We refer to this measurement as inertia or mass (Fig. 1), but never as quantity of
    matter.
Adapted for the Internet from:

Why God Doesn't Exist
Quantum ‘predicts’
the existence of a
unit of matter!

    The parameters that Taylor and Wheeler invoke to excuse their inability to express mass in terms of
    quantity of matter lend support to my argument. Parameters such as temperature and radioactive decay
    are intrinsically dynamic concepts and defeat the quantity of matter definition by default. These relativists
    are attempting to determine quantity of matter through measurement. A particle is a photograph and not a
    movie, and the number of indivisible units that comprise a particle at that particular cross-section of time
    is countable. But if we were to count units instead of measuring parameters, where would this leave our
    arrogant mathematicians? It would reduce their lofty discipline of functions and equations to a daycare
    game of blocks. Hence, Quantum Mechanics has a built-in contradiction. It can never discover the
    fundamental particle it postulates because it searches for and attempts to establish this unit through
    measurement.


    2.0   Le Grand Variable

    One conspicuous result of relying on measurement as opposed to counting units is that we end up with
    a variable unit of mass known as the kilogram. This standard consists of a chunk of metal that sits
    in France and which everyone affectionately calls ‘Le Grand Kilo.’ [2] It is in reference to fractions or
    multiples of ‘Le Grand’ that we specify mass and not with respect to a hypothetical unit of matter. Thus,
    the definition of mass of relativity turns out to be another of those self-serving dualities that
    mathematicians love so much. It embodies the irreconcilable concepts of quantity of matter and of inertia.
    The mathematicians have no use for and reject the ‘quantity of matter’ definition, but insinuate in all their
    writings that this is what they mean. For instance, relativists specify the mass of the electron in kilograms
    (Me = 9.11 × 10-31 kilograms), [3]  which would suggest that we are referring to quantity of matter because
    we pegged it to Le Grand. However, if we take Le Grand to the top of Mount Everest it would not weigh a
    kilogram. Changing its location on Earth changes its weight, which changes its mass because we
    determine mass by weighing the object. And even this realization is trivial in relation to the punch line that
    follows. According to the experts at Weights and Measures, even if we cut ‘Le Grand’ in half, one of these
     pieces would still weigh one kilogram:

    " By definition, the error in the repeatability of the current definition is exactly zero…
       The international prototype of the kilogram seems to have lost about 50 micrograms
       in the last 100 years, and the reason for the loss is still unknown…It is accurate to
       state that any object in the universe (other than the reference metal in France) that
       had a mass of 1 kilogram 100 years ago, and has not changed since then, now has
       a mass of 1.000 050 kg." [4]

    So what is the true mass of the electron if it is pegged to a variable?

    It is these types of ambiguities that have prompted relativists to devise ever more irrational definitions of
    the word mass. Specifically, they had to invent two different types of masses, one known as rest mass
    and the other known as relativistic mass. There was no other way to accommodate their pet peeves. The
    rest versus relativistic mass debate raging in relativity forums is the most conspicuous example of this
    duality. At the heart of the dispute is whether it is the quantity of matter of a traveling object that increases
    or just its velocity. The conveniently vague definition of the strategic word mass guarantees a massive,
    circular debate.

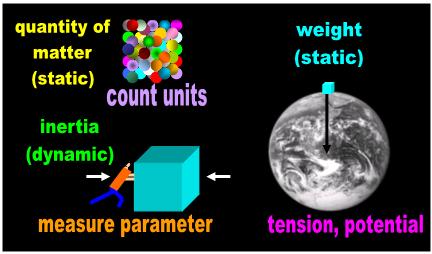
Fig. 1   Mass Duality: The two definitions of mass
The ‘quantity of matter’ definition
of mass is conceptually static. This
definition has to do with the units
of matter that comprise an object in
a cross-section of time irrespective
of observers. The ‘inertia’ definition
of mass, on the other hand, is
intrinsically dynamic. In order to
conceptualize inertia, the object has
to move.
Beats me, Steve!
I'm just a peasant!
I just don’t understand it, Bill,
and I've done the experiment
over and over! I cut and divide
each piece in half, and I always
end up with something.



    ________________________________________________________________________________________


                                  Home                    Books                    Glossary            




        Copyright © by Nila Gaede 2008