My ruler can contract,
but not its length!

    1.0   We don't need Math to solve this one

    The first thing you should come to grips with is that we don't need variables or equations to analyze and resolve relativity's
    ridiculous claim that length contracts. The conclusion that the mathematicians are offering are of a qualitative nature. They
    are saying that, because a muon travels 'fast', length and distance contract. Why would we need to invoke meters and
    seconds to explain such a qualitative phenomenon of nature? If I tell you that when I throw the ball at you, the distance
    between you and the ball is going to shrink, would you ask me to get a calculator to prove it to you? Do you think that your
    doubts about my claim would vanish after running an experiment? This is entirely a conceptual issue. Unless the relativists
    can show a reason why I need a calculator or a slide ruler, I will resolve it with logic.

    Like Einstein, I will resolve it with a thought experiment. Why should he be allowed to use a thought experiment and not you?  
    If the thought experiment shows that the idea is patently absurd, we have no alternative but to scrap it. Why would anyone
    require you to learn Math to solve this one? In fact, before a mathematician can design, let alone run an experiment, he must
    verify whether it violates logic. He would be unable to run the experiment in the lab if he cannot even conceive of it in his
    brain. Logic always precedes Math, DOE, and experimentation. The mathematician can prove anything with numbers. The
    question is whether we can run his proposal in the lab. And before we can run it in the lab we need to conceptualize and
    visualize the proposal. So let's check the logic of what the mathematicians are proposing to make sure that they crossed
    all the t's and dotted all the i's.


    2.0   Relativists should make it a goal to take English 101 sometime in their careers

    A boy measures five feet. We refer to this parameter as his length or height. We determined this because we took a
    measurement of the boy and not because we took a measurement of his length! The mathematicians may argue that my
    pants have a certain length and that if I put my pants in hot water they can shrink. The mathematicians may not argue
    that the length of my pants contracted.

    Relativists will scoff that this is a trivial semantic objection. Yes, many writers abuse the language and perhaps overindulge
    in metaphor and analogy, but this doesn’t invalidate Einstein’s mathematically exact conclusions. Surely, we can read
    between the lines and get through the poetry to understand what the writer is really saying.

    Actually, there is more to the term ‘length contraction’ than meets the eye and than relativists realize or wish to
    acknowledge. More than a semantic this is an epistemological issue. Relativists have vital reasons for using the word
    length and not the word object. Mathematical length is a quantitative, subjective parameter. The physical shrinking of my
    pants is a qualitative, objective matter. We do not need an observer to testify that a pair of pants contracted. The pants
    shrunk or not irrespective of our state of knowledge. Relativists purport to derive qualitative inferences from quantitative
    foundations. The quantitative ones require mathematical symbols. The qualitative ones only require English, unambiguous
    definitions, and usage consistency. By invoking the word length, the mathematicians stealthily and without justification
    redirect the discussion towards magnitudes, variables, and equations when the instant issue is entirely conceptual.
    Neither measurement nor calculations will resolve the length contraction paradox. Relativists are in effect answering a
    yes or no question with a ‘how much’ reply, thus implying indirectly – rather than stating explicitly – that the object
    contracted. This explains why so many Physics forums still debate whether length contraction is 'real' or a matter of
    perceptions and appearance.

    Take for instance the situation where your cap falls in the lake. You grab a long tree branch you find on the ground to
    retrieve it from the waters. You did not need a calculator or to learn calculus to determine how long the branch should be.
    You established this intuitively. Of course, your intuition may fail, in which case you don't recover your cap. But this is not
    the point. The point is that if you manage to retrieve your cap it is because of qualitative as opposed to quantitative length.
    You don't need to know how many feet or meters the branch measured to explain to me how you recovered your cap. You
    either did or didn't. The branch was either sufficiently long or it wasn't. This is qualitative length. This is the sense of the
    word length in Physics.    

    So, does the Lorentz equation say that a ruler contracts (independent of observers) or does it say that its length as
    measured by an observer changed? One is objective. The other is subjective. Which is it going to be?

    The reason relativists often disagree amongst themselves as to whether ‘length’ contraction is real or apparent is that
    they rely on subjective observers for all of their physical interpretations. They cannot tell you whether the object at the
    other side of the Universe shrunk. They can only tell you what an observer measured or should have measured. As in
    all charismatic religions, without testimonials, relativity is dead! The fact that every relativist uses the same metaphors,
    analogies, and words to explain SR theory makes their invocation of the word length even more suspicious. Jargon is
    a symptom that cult members take concepts for granted.
Adapted for the Internet from:

Why God Doesn't Exist
I thought you said
that the length of
the ruler contracted!

    3.0   Thank God for flexible definitions!

    The epistemological shortcomings of relativity become even more pronounced from the inconsistent use of the word
    length. A wooden board is made of small particles called atoms, and the mathematical establishment holds that atoms
    are made of smaller particles yet.

    “ it is now known that the atom can be broken down into a number of smaller
       components.” [1]

    The mainstream hypothesizes that atoms are mostly empty space:

    “ Rutherford’s backscattering experiment] demonstrated that atoms consisted
       of mostly empty space”[2]

    If we add that between atoms there is yet more space, consensus is that a board is mostly empty space.

    “ Ordinary matter, or the stuff we and everything around us is made of, consists
       largely of empty space. Even a rock is mostly empty space.”[3]

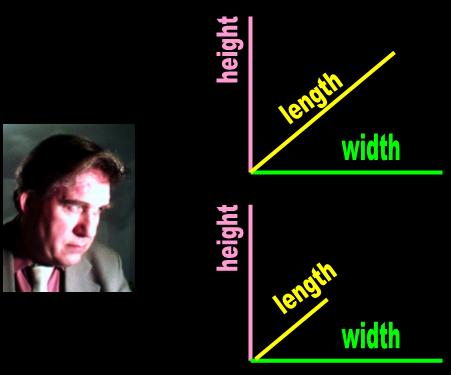
    However, when mathematicians measure and report the results of the length of a board, they do not subtract the empty
    space from the balance (Fig. 1). They include the entire magnitude as if the object had no ‘space bubbles’. In the context
    of the word length, a board is made of a single piece. From a conceptual point of view, mathematical length is continuous.
    On the other hand, distance is the amount of space between two surfaces. Distance refers to the emptiness that separates
    two particles or objects. Distance is qualitatively different from length because it includes only the ‘space bubbles’ and
    none of the matter! If matter refers to what is, distance alludes to what isn't. Whereas length is conceptually continuous,
    distance is conceptually discontinuous. Length is all matter and no space; distance is all space and no matter. And
    whereas length between the ends of a conceptually continuous object cannot shrink, the measured distance
    (i.e., distance traveled) between two distinct objects can hardly ever be constant.

    The qualitative difference between length and distance now sets the stage to understand what the mathematicians are
    doing with their length contraction theory. Relativists are not talking about length contraction, but about decrease in
    distance between particles comprising an object. Relativists are not talking about matter. They are talking about the
    space separating the surfaces of two or more objects. This is a little more than just a semantic objection. Length
    cannot contract because it is conceptually made of a single piece. The word length implies that the object is perfectly
    rigid and has no space bubbles. If at all, it is distance which can vary. If relativists have for 100 years used length instead
    of distance to explain this aspect of their theory it is because they forcefully attempt to apply their stupid equation not
    to motion or to location (distance traveled, separation) as they should, but to architecture. They are using a displacement
    equation (dynamic) in the context of a static scenario: the length of an object.

    The reason our bright mathematicians have failed to identify this drawback to their theory is again language. The
    mathematicians define their key words loosely and then amend them retroactively in the middle of the dissertation.
    In high level Mathematics, length is a synonym of distance:

    “ In the physical sciences and engineering, the word ‘length’ is typically used    
       synonymously with ‘distance’, with symbol l or L.”[4]

    Mathematicians define length as the ‘distance’ between two points and distance, as the ‘length’ between two points.
    As far as the mathematicians are concerned, they have to unroll the measuring tape whether they measure length or
    distance, so what the hell is the difference? To them, both length and distance are dynamic. Therefore, relativists
    have never found a need to develop physical definitions of these terms or to emphasize their qualitative differences.
    The mathematicians have developed only subjective, artificial, and measurement-related definitions of length and
    distance. This is the root of Special Relativity’s supernatural length contraction conclusions. The other half of the
    problem has to do with the eternal bad habit the mathematicians have of relying on circular definitions. In Mathematics,
    a length is a distance and a distance is really a displacement.
Ooooh! Now
that's scary!
the day length contracted



    ________________________________________________________________________________________


                                  Home                    Books                    Glossary            




        Copyright © by Nila Gaede 2008