| Adapted for the Internet from: Why God Doesn't Exist |
| The mathematicians invented negative direction |
- 1.0 Direction belongs exclusively to Physics
The first quantitative (mathematical) concept discovered by civilization was probably the positive integer.
[1] [2] At some point in Paleolithic time, Man began to count apples and oranges and to represent the
results with tally marks. [3] Eventually, man assigned symbols known as numerals to differentiate these
quantities. [4]
Merchants and traders later developed negative numbers, partly from the necessity to record debt in
accounting transactions:
- “ For purposes of addition and subtraction, one can think of negative numbers
as debts. Adding a negative number is the same as subtracting the corres-
ponding positive number” [5] [6]
In other words, the minus sign (-) is not really a mathematical concept such as a number, but a symbol
that represents an operation. Negative simply meant that you owe the amount to me.
In retrospect, it was predictable that the mathematicians would sooner or later extend the notion of
'negative' to direction:
- “ vector: A mathematical entity that has both magnitude (which can be zero)
and direction.” [7]
“ vector: In physics and in vector calculus, a spatial vector, or simply vector,
is a concept characterized by a magnitude and a direction.” [8]
“ If the scalar is negative, it also changes the direction of the vector by 180º.” [9]
In the context of vectors, ‘negative’ means contrary motion. A minus sign prefixed to a vector quantity
indicates that the motion is in a direction contrary to a reference. Therefore, if you travel 3 kilometers
southwards and retrace your steps 1 kilometer northwards, you traveled a net distance of 2 kilometers
southwards from your point of origin (Fig. 1).
The mathematicians got into the habit of symbolizing vectors with little arrows. The arrow is supposed to
represent an itinerary, a bunch of locations. In the foregoing example, the arrow pointing south is thrice
as long as the arrow pointing north.
There are, however, fatal problems with this symbolism:
- measured in units such as meter per second or miles per hour.
- • The arrowhead represents direction, a static and qualitative concept. Direction
- should not and does not involve Mathematics.
- • Distance traveled is segmented whereas direction is continuous – ‘made of a
- single piece.’ We can chop and hack kilometers and kilometers per hour into
discrete little pieces. We cannot divide direction even in half.
Hence, it is ludicrous to attempt to synthesize distance-traveled and direction with a single line as the
mathematicians do routinely.
But the insanity of Mathematics doesn’t stop here. The truly amusing part of the Math show comes up
when you travel 3 kilometers south and retrace the same 3 kilometers north. The idiots of Mathematics
'illustrate' such operations with null and position vectors, which from a physical point of view can only
mean that the object moved and returned to origin (dynamic) or that it never left in the first place (static):
- “ In physics, moving position vectors are used in mechanics and dynamics
to keep track of the positions of particles, point masses, or rigid objects.” [10]
[Moving positions? Oh man, this is getting scary!]
The Wolfram site speaks volumes regarding the insurmountable troubles the mathematicians run into
when they attempt to illustrate null and position vectors. The page that defines the word vector depicts
an arrow that symbolizes magnitude and direction. [11] The vector is labeled with the words head and
tail. The page that defines the null vector shows absolutely nothing. [12] The null vector has neither
head nor tail, poor fella! The null vector is… how can I say this… an arrow-less arrow (Fig. 2). If ever a
mathema-tician defines a vector as having magnitude and direction and illustrates it with an arrow, ask
him to draw for you a null vector. Insist on seeing the arrowhead so you know in which direction you
are not moving.
What this shows, again, is that the magnitude of a vector is exclusively a mathematical concept. The
direction half of a vector is exclusively a qualitative physical interpretation of the operation. Indeed, the
same is true of every operation in Mathematics. Whether we add, subtract, multiply, divide, raise a number
to a power, or take a square root, the amounts belong exclusively to Mathematics. The operations and their
physical interpretations belong exclusively to Physics. If you have 3 shoes and the thief takes away 2 of
them, we still have three shoes. They are just apportioned differently. They are merely in different locations.
Destroying the two is not the same thing as 'taking them away.' Subtract means to withdraw, not to annihilate.
Likewise, adding refers to existing shoes, not to the act of creating them. You must have shoes before you
add or subtract them.
We have to conclude that direction has absolutely nothing to do with Mathematics, which means that the
mathematician is statutorily barred from defining this strategic word. Mathematics has no use for qualitative
concepts such as direction any more than it has use for concepts such as love or justice.
In a scientific context, direction is a qualitative physical interpretation of a mathematical operation
which the mathematicians in their immense ignorance symbolize with a negative sign.
2.0 ...yet no one in 'Physics' defines the word direction
Having said this, it doesn't come as a shock when we fail to find a formal definition of the word
direction in specialized dictionaries or encyclopedias of Physics where it belongs. You will not find
the word direction at the Wolfram Physics site [13] or at the Infoplease Encyclopedia of Physics. [14] You
will not find it at the Wikipedia under Physics. [15] Where you will find 'examples' of direction is
in a dictionary of Mathematics:
- “ signed number: a number preceded by a plus (+) or minus (-) sign, indicating
a positive number (+) or negative number (-). Signed numbers are also called
directed numbers since the sign can indicate position (or direction) of a
number, relative to zero on a number line.” [16]
“ The direction from an object A to another object B can be specified as a
vector v = AB with tail at A and head at B. However, since this vector has
length equal to the distance between the objects in addition to encoding
the direction from the first to the second, it is natural to instead consider
the unit vector v (sometimes called the direction vector), which decouples
the distance from the direction... The direction from an object A to another
object B can be specified as a vector v= AB with tail at A and head at B.” [17]
“ A direction is determined by an ordered pair of two numbers (a,b), not both
zero, called direction numbers. The direction corresponds to all lines parallel
to the line through the origin (0,0) and the point (a,b).” [18]
Actually, the famous direction the idiots of Mathematics are talking about has nothing to do with direction. It
has to do with the particular way in which numbers increase or decrease on a number
line. In Mathematics, the word negative simply means less than zero.
- “ Keep in mind that a positive y direction is up, a negative y direction is down,
a positive x direction is right, and a negative x direction is left.” [19]
[These are just conventions. The number line of Math can be placed diagonally
if I wish. The alleged 'direction' in which the arrowhead points merely indicates
that numbers increase.]
- But what location or position does zero have? How would the mathematician know that the negative direction
is towards the left if he has not yet defined the word direction? The words left and right may qualify as
examples of directions, but not as definitions. Before the mathematician can use the word direction in a
sentence he must define it. Indeed, it is the mathematicians’ insistence on regarding direction as a
mathematical concept that explains why this word remains undefined. The definitions of Mathematics are not
definitions, but rather proofs. The mathematicians have never defined a single word in their entire vocabulary.
Mathematics is not founded upon definitions, but upon axioms. [20]
3.0 The scientific definition of direction
The task before us, then, consists of defining the word direction for the purposes of Physics. We
should expect a wholly qualitative definition which we are going to use to provide a physical interpretation to
a phenomenon. Since mathematical physicists rely on non-scientific notions that
English majors have developed over the years, this is a good place to start.
The most popular meanings of the word direction include:
- 1. The course along which something moves, aims or points.
2. A line leading to a place or point, or along which something lies, aims or points.
3. To aim or move along a line.
4. A position to which motion or another position is referred.
5. The alignment of two points in space, or their mutual angular position, or orientation.
Unfortunately, these definitions are too vague and have mutually conflicting elements to be used consistently.
Some emphasize a target, but lack an itinerary. Others have it the other way around.
The last one is a tautology: direction = alignment.
The absence of rigor creates communication problems during the physical interpretations of
mathematical theories. For example, what can Weyl mean when he states that ‘a curve preserves
its direction unchanged’ ( p. 115). [21] Or what is the significance of Heidemann's statement that we
can go around the Earth always in the same direction (p. 71). [22] Evidently, Weyl and Heidmann are not
referring to a rectilinear displacement towards a stationary target. They implicitly equate direction with forward,
casually relying on the ‘course along which something moves’ or ‘to set or hold a
course’ definitions. Specifically, the examples offered by Weyl and Heidmann fail to meet the ‘straight’
requirement of the definition of direction. Therefore, we definitely must come up with a definition of
the word direction that can be used consistently.
But is this really a problem? Doesn't it all boil down to the prosecutor's choice of definitions?
It becomes a problem in Physics when we run up against misguided conclusions founded on such statements.
Hawking claims that time points or flows in the ‘forward’ direction and depicts this parameter with a straight
axis capped by an arrowhead that he says points towards the ‘future.’ If the future is the ‘direction’ in which an
object moves when it moves forward, do flanking motions to the
left and to the right qualify as directions towards the present in his model? Is backward motion a direction into
the past? Is my future direction your past direction when we meet head on? If a balloon expands radially,
which part of the surface is moving in the direction of the future?
For instance, we can rephrase Heidemann’s description and say that we move around the Earth by walking
‘forward.’ Or we can rephrase and say that Weyl meant that the last point on a curve is ahead
of the one preceding it. What these statements indicate is that you are transferring your eyes to this next-to-
the-last point and looking ‘forward’ at the back of the other. The jury would get a vague idea
that, by 'direction,' the presenter actually means ‘forward.’ But what can the jury understand when
the prosecutor clarifies that time flows or points ‘forward’ or in the direction of the future. We have a concept –
time – facing in the direction of another concept – the future. So where is this physical
object called 'future' located? If direction belongs to Physics, there absolutely must be a physical object
underlying the concept direction and this object must have a location. Time by itself has
neither direction nor location because this word does not depict a physical object. Nevertheless,
isn’t it incumbent upon the prosecutor to define the term direction if it is such a fundamental concept
of Physics? Or, to see things in light most favorable to relativists, shouldn't we define direction if, as
they say, it is an essential component of their mathematical vector?
The unscientific usages of direction that I just alluded to are not a complete loss, however. They nevertheless
serve as a basis to determine what attributes a direction should or must have. A
direction:
- • should embody a location but make no provision for motion
• must point parallel to a straight line, specifically, to the line of sight
• must make a provision for a target. (i.e., involves two objects.)
• must be objective rather than subjective, defined rather than proven
- (i.e., it shouldn't involve an observer).
- • must make a provision for aiming, pointing, facing and tilt.
Let's analyze each of these attributes and see if we can incorporate them into a definition of direction that we
can use consistently in Science.
- Location
Direction is conceptually static and indivisible. We cannot divide direction in half, chop it into little pieces, or
construct it with discrete components. When we invoke motion, we imply a minimum of
two locations, meaning two frames in the cosmic film. A mathematician may get away with saying that he can
place a straight line between two static points. His argument is guaranteed to fail if he claims
that two successive locations of one object constitute a straight line or rectilinear itinerary. With
respect to what? With respect to Jupiter? The only way we can depict direction is with a continuous straight
line. This cannot involve more than one frame in the movie.
Straight
In Physics, the word straight roughly means:
- “ the quality or state of extending in one direction without turns, bends or
curves; or being without influence or interruption.” [23]
“ A curve is a line no part of which is straight.” (p. 112) [24]
- These are not perfect definitions, but they capture the essence of what most people understand by
the word straight. Therefore, by definition, a curve does not have direction – no portion of it lies
entirely along the line of sight.
Of course, the mathematical physicists couldn’t use this definition. It stood in the way of their supernatural
physical interpretations. So they got around it by incorporating straight under the definition of curve:
- “ In mathematics, the concept of a curve tries to capture the intuitive idea of a
geometrical one-dimensional and continuous object. A simple example is the
circle. In everyday use of the term "curve", a straight line is not curved, but in
mathematical parlance curves include straight lines and line segments.” [25]
“ A line can be described as an ideal zero-width, infinitely long, perfectly straight
curve (the term curve in mathematics includes 'straight curves')” [26]
No one but an idiot of Mathematics believes that a straight line is also a curve. What meaning could such
nonsense have? In the rational world of Physics, curved and straight are antonyms.
The mathematical definition of the word curve nevertheless reveals the true intentions of the
mathematicians. They are not talking about the 1-D, about continuous, about an object, about a
curve, or about straight. They are talking about itineraries that deviate from a rectilinear path. They
are not talking about curved, but about curvilinear. A ball is curved. When the batter strikes it, the
ball moves curvilinearly. The straight line of Mathematics is purportedly a trajectory, a movie of a
dot supposedly traveling in a ‘straight line’ from one frame in the cosmic movie to another.
However, in the real world, not a single object travels rectilinearly, for I ask, with respect to what? In Physics,
it is surrealistic to speak of rectilinear itineraries. The only context in which we can say that
the Moon moves in the direction of the Andromeda Galaxy or that the gun is pointed in the direction
of the target is in a static context. We must visualize the Moon and the gun standing still and facing
the target straight ahead along the line of sight perpendicular to the selected plane. Again there must
be two objects and the scene must be static. If the mathematician invokes a second frame, the movie
is guaranteed not to have 'direction.'
Two objects
The problem with the word forward is that the object uses itself as a reference. A lonely object in the Universe
may be conceived as pointing forward – just choose a face – but we still know nothing
about direction. The word direction implicitly invokes a second object. A line tangent to a sphere
may have direction because we reference one end against the other, but what is the direction of the lonely
‘point’ it allegedly touches if we consider it all by itself? In what direction does any point on
the surface of a sphere point or face? Until we have a second object that serves as a reference, we
still do not have direction. Words such as forward, future, and up are neither objects nor locations.
They stealthily use a preferential tilt or orientation of the object at the center of attention as a
reference. They tell us nothing about either the itinerary or the destination of this object. In Physics, there are
no directions such as love or happiness. Qualifiers such as northward or eastward stealthily embody extrinsic
objects as a reference. On Earth, northward means toward the North Pole. In this context, the mathematician
treat the North Pole as a physical object. But the object that is pointed towards the North Pole tacitly does it
through the body of the Earth, not along its surface. A geodesic may consist of forward motion, but it does not
have direction. Its direction changes in every frame of
the movie.
Objective
The word forward is also a poor criterion to define direction because it has subjective connotations.
It depends on an observer. Your forward direction is not the same as mine. Therefore, the jurors have
to second-guess the prosecutor and fill in the blanks on their own. Direction, on the other hand,
should not be an issue that needs to be decided with an experiment. The words aim, point, and face
are objective. The barrel of the gun is either physically tilted towards the target or it isn’t. Opinions
have no bearing on the reality of whether it is or not. Likewise, the Milky Way either moves or doesn't
in the direction of the Andromeda Galaxy. We don't need a conscious observer to measure whether it does or
not. The definition of direction cannot have us second-guess whether the rocket intends to curve towards the
North Pole when it travels tangentially to the Earth. Only in each individual frame of this movie can we talk
about direction. We can say, for instance, that in a given frame the rocket is traveling in the direction of Mars.
Hence, the static and objective word straight can be used to define direction and not the subjective word
forward.
Aim, point, face, and tilt
The word face derives from the Latin facies meaning the surface at the front of the head. The verb ‘to face’
derives from this noun and refers to the alignment of the body with the plane of the face. We
have extrapolated this notion to objects. We say that a cube faces the wall, meaning that we momentarily
substitute our face – more specifically our eyes – for the plane in question and look out from it. The verb to
face reduces to offering an imaginary plane perpendicular to the line of sight.
For instance, the cue of a game of billiards has what we refer to as a ‘point’ at the tapered end. When seen
head on, this tip is not typically characterized as facing, but as pointing. Upon closer inspection, however,
the tip of the cue is a surface, indeed, much larger than the surface of the tip of a pin. But then, even the tip
of a pin shows up as a surface under the microscope. And so does the surface of a hydrogen atom! There
is not a single real object in the Universe that will not exhibit a surface under the right magnification. Hence,
for the purposes of Physics, the words facing and pointing are synonyms. We are treating the surface in
question as a plane, substituting our eyes for this plane, and looking outwards along our line of sight. Face
and point are not verbs, but static attributes like tilt and orientation. The object does not occupy more than
one location when it faces or points. Facing differs from direction in that it implies self-reference. Direction
requires an extrinsic reference. If facing means 'to look,' direction means 'to see.' We can replace direction
with a straight line, but we cannot do the same with facing or pointing. The word tilt, in comparison, is the
position of the object from another object's perspective. Here the observer places his eyes on the target
rather than on the source. It is the merging of face and tilt that imbues direction with reciprocity.
Let's put it all together now.
- facing or pointing: Imaginary substitution of a specific plane of an object with
the observer's eyes. (v.) To look outwards.
tilt: The face an object presents from a particular perspective.
direction: Line of sight. The mutual facing of two objects; a conceptual linking
of two locations. Direction is a property of straight lines and edges.
Direction and facing emphasize the source. We are placing our eyes on the source object. Orientation and tilt
emphasize the target. Our eyes are on our face again staring at the target from afar.
The following statement synthesizes the meaning of direction:
- “ The book is tilted in such a way with respect to the ceiling that if I place my
eyes on that specific face of the book, I would see a spec in the ceiling and
vice versa.”
Dr. Math asks rhetorically whether it is possible to define the word direction without using the words point
and line:
- “ Your definition would require us to first define 'ray' and 'direction.' Can you
do that without reference to 'point,' 'line,' and 'plane'?” (p. 5) [26]
Here I showed Dr. Math that we can. Therefore, students don't need to take Math 101 to understand what a
direction is. It suffices that they take English 101. The reason relativists have never formally defined direction
despite that they use the word in so many of their writings is that they have not realized the importance of
language to the scientific method. They give lip service to the word rigor and use definitions inconsistently
anyways. Without proper definitions, the prosecutor is talking about a rock and the jury is visualizing a tree.
Fig. 1 Minus Vectors |

What is it that you don't
understand, Bill? This is
positive direction, this is
negative direction, and this
is zero direction.
understand, Bill? This is
positive direction, this is
negative direction, and this
is zero direction.

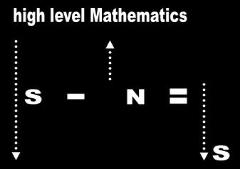
| The mathematicians depict displacement with arrows they call vectors. Therefore, if you subtract 1 mile north from 3 miles south in the religion of Mathematical Physics, you end up with 2 miles south. That’s the net magnitude and direction of your displacement. |
| The problem is that direction is conceptually static and made of a single piece (i.e., a photograph). We cannot chop direction into pieces. Magnitudes and displacements, on the other hand, are divisible. A magnitude is the result of counting (i.e., a movie). Displacement involves several frames of the Universal Film. Therefore, it is ludicrous to attempt to synthesize the magnitude of a displacement and direction with a single line. The magnitude of a mathematical vector belongs exclusively to Mathematics. The direction part of the mathematical vector belongs exclusively to Physics. Never the twain shall meet. So now for the amusing part... |
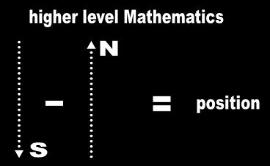
| Fig. 2 Null and position vectors |
- Module home page: A mathematician has no idea what a dimension is
Pages in this module:
1. This page: The mathematicians invented negative direction
2. The only structural concept that is 1-D is an edge
3. A mathematician confuses straight with rectilinear
4. The mathematical definition of dimension is unscientific
5. A mathematician says that a coordinate is a dimension
6. A mathematician says that a vector is a dimension
7. The dimensions, coordinates, and vectors of Mathematics are really number lines
8. Time is a number line, not a dimension
| If you travel 3 miles south and then 3 miles north and arrive at your starting point, the mathematician says you never left. He depicts these non-motion type of operations with null or position vectors, which is no vector at all. The null or position arrow of Math doesn't even have an arrowhead, for in which way is 'position' moving or pointing? So the next time you visit your local mathematician, ask him to illustrate a nulll vector for you. Let's see what he draws. |
- ________________________________________________________________________________________
- Copyright © by Nila Gaede 2008
