The mathematicians routinely claim that dimensions have a property called size.
- " the spatial dimensions grow or stretch as the universe gets older." [1]
"The distance a particle can travel before reaching its initial position is said to
be the size of the dimension." [2]
The dimensions of relativity thus grow when a balloon expands...
" the field acts as an engine that inflates th dimensions of cosmic space (p. 359) [3]
shrink to infinitesimal size...
" The compactified coordinate θ runs from 0 to θ0. As t runs from - ∞ to + ∞, the
compact dimension shrinks away" [4]
or, in extreme situations, disappear altogether...
- " At some point in the past the radius was zero (infinite curvature) and from this
state it expanded…this… is the basis of the Big Bang theory." (p. 80) [5]
" At the big bang itself the universe is thought to have had zero size (p. 117)
a star collapsing under its own gravity is trapped in a region whose surface
eventually shrinks to zero size" (p. 49) [6]
- Hawking adds that he conceives of a zero size Universe, i.e., no length, width, or height. p. 44. He claims
that Penrose proved that a star collapsing under its own gravity shrinks to zero size, what he refers to
as a singularity or a point in space-time where curvature becomes 'infinite'. Hawking, 1988, pp. 49 – 51.
Other relativists have the same opinion:
" the Universe was "shrunk down to nothing at all." (p. 658) [7]
Such statements coming from leading physicists are appalling. I have a hunch that laymen will also
have trouble visualizing the infinite curvature of a zero-radius object. Perhaps in the religion of relativity
circles and spheres can have zero size, but not in Physics! Whatever is alleged to have a zero radius
can be classified as neither circle nor sphere, but as nothing. So far relativists have talked about 0, 2,
and 3 dimensional Universes, but there is no sign yet of the promised 4-D.
This quantitative attribute was likely extrapolated from the lay world where it is common to ask for the
dimensions of a box. Of course, this is quite a different pursuit than if the person had asked whether the
box is three-dimensional. But what can size mean in the context of dimensions? Are we saying that a
line becomes longer or shorter or that a magnitude changed?
If relativists are referring to a magnitude, they are at best talking about a number line. If, instead, they
are talking about a physical line that shrinks or expands, this line must necessarily be segmented. Each
discrete point appears or disappears in a new frame of the film, which means that relativists are neither
talking about a line nor about a dimension, but about a vector. Indeed, in relativity, the size of a
dimension refers to the distance traveled by a particle. [4] If this distance is now quantified, then our
mathematicians are not even talking about a vector, but again about a number line, especially if the
dimension shrinks to the point where it disappears altogether. Only a direction-less number line may be
conceived to be 0-size, i.e., zero distance traveled. If the physical dimension of width were to shrink to
0-size, instead, the solid would convert to a plane or the plane to an edge. Such surrealistic images
don't belong in Physics but in religion. There is no standalone plane or edge in the real world. Perhaps
in Mathematics dimensions may shrink and grow, but in Physics all three dimensions always have the
same 'size'.
The mathematician asks qualitative questions:
- 1. What is the large-scale structure of the Universe?
2. is Space-time an object?
3. What is a black hole? Are black holes now considered to be 'proven' real objects
in the universe?
The mathematician does not answer that the question of the structural nature of the Universe by saying
that it is spherical or cubic. He answers that it is uniform, homogenous, and that it is clustered or he
phrases them in mathematical form. He jumps incessantly from Math to Physics and back again.
In other words, he is not interested in whether answer that the Universe has the shape of
- “ A black hole is a region of space-time into which matter has collapsed, and out
of which light may not escape…this escape horizon has a very sharp boundary
in space called the Event Horizon. There is a precise mathematical prediction of
the radius of this horizon which for objects that do not rotate, depends only on
the mass of the body that has fallen through its event horizon. It is given by the
formula…” [8]
The mathematician ends up responding to a ‘what’ question with a description in terms of mathematical
symbols. He gives you a theory of an object, of how the mathematician inferred that there is such an
object or that Mathematics predicts the existence of such an object. Then the mathematician goes to the
next level. He proves to you that an object exists:
- “ I think the circumstantial evidence for the existence of black holes is now so
strong that it would be hard not to consider them to be real objects in the
universe…I have watched the evidence mount during the last three decades
with astonishing speed, culminated by the fantastic observations by the
Hubble Space Telescope. It is hard to imagine that some other mechanism
can be the host for the phenomena we see in the cores of quasars and active
galaxies.” [9]
When you ask him about the definition of a black hole, he tells you that your question is a subject of
Philosophy.
However, in Science, we don’t prove existence. We first define the word exist, and then an object exists
or doesn’t depending on whether it meets the criteria of the definition.
- “ The length of the cuboid is 12cm, its width is 7cm, and its height is 3cm… ” [10]
“ The distance between two points is the length of the path connecting them. ” [11]
“ The length is the longest dimension of an object. ” [12]
[The longest dimension? I guess this is what the mathematicians are alluding to
when they say that their definitions are 'rigorous.']
“ The width of a box is the horizontal distance from side to side ” [13]
“ height: The vertical length of an object from top to bottom. ” [14]
“ So the question is, where are these extra dimensions? One suggestion is that they're
all around us, but they're small relative to the dimensions that we directly see and
therefore are more difficult to detect.” [15]
[ How big is width? If Greene was perchance talking about mathematical dimensions,
what could he possibly be referring to? He must have seen a ghost ‘all around’ his
bed.]
“ A 2D surface looks 1D when its radius is small…we therefore assume that 6 spatial
dimensions are 'curled up" on themselves, while the remaining 3 dimensions extend
to infinity (or at least to very large distances)…a manifold that is "curled up" in the
way that we desire is called 1compact1” [16]
[ How do you curl height? Does height extend a mile or two?]
“ the other dimensions are curved up into a space of very small size, something like a
million million million million millionth of an inch. This is so small that we just don’t
notice it: we see only one time dimension and three space dimensions, in which
space-time is fairly flat. It is like the surface of a straw. If you look at it closely, you
see it is two-dimensional (the position of a point on the straw is described by two
numbers, the length along the straw and the distance round the circular direction).
But if you look at it from a distance, you don’t see the thickness of the straw and it
looks one-dimensional (the position of a point is specified only by the length along
the straw).” (p. 163) [17]
“ the spatial dimensions appear to grow or stretch as the universe gets older” [18]
[ How do stretch width? I thought the other guy said it already runs to infinity.]
- Dimensions have size? What size does width have? How far does height extend to? Length grows?
You mean like a plant? How many inches does it grow by?
What are the idiots of Mathematics babbling about? They lost touch with their subject matter hundreds
of years ago.

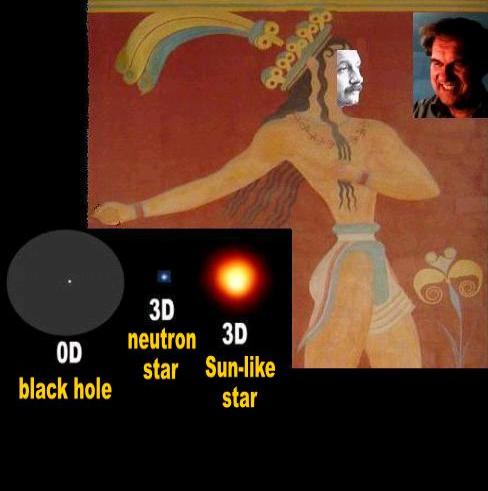
| Ha, ha, ha. That was very funny, Al. Now really, what happens to a large star? |

| This is a 3-D star like our Sun, Bill. If a star has a lot of mass, it turns into a tiny 3-D neutron star like this little blue one. And if it has more mass, it turns into a 0-D black hole like this third one. |
- Module home page: The mathematical definition of dimension is unscientific
- Pages in this module:
- 6. This page: The mathematical dimension of length has zero size
| The mathematical dimension of length has zero size |
| Adapted for the Internet from: Why God Doesn't Exist |
- ________________________________________________________________________________________
- Copyright © by Nila Gaede 2008
