| The multi-dimensional 'number of numbers' definition of Math is unscientific |
| Adapted for the Internet from: Why God Doesn't Exist |
Perhaps to introduce the problem with dimension it is best to proceed with an example where the word is
used inconsistently in the same presentation by experts. If they don’t know, much less can we expect lesser
mortals to know.
One of the best examples of usage inconsistency is found in Hawking's popular book, where he gradually
reconstructs the process by which relativists derived that space-time is four-dimensional. Beginning easy
on the lay reader, Hawking applies the formal definition in a 2-D context. He tells us that:
- “The surface of the Earth is two-dimensional because the position of a point can be
specified by two coordinates, latitude and longitude.” (p. 2x) [1]
Hawking also provides a quantitative and a qualitative 3-D example:
- “ For instance, one can say that a point in a room is seven feet from one wall, three
feet from another, and five feet above the floor. Or one could specify that a point was
at a certain latitude and longitude and a certain height above sea level.” (p. 2x) [2]
These are not only his opinions. The Wolfram site has a similar version:
- “ dimension: the number of coordinates needed to specify a point on the object. For
example, a rectangle is two-dimensional, while a cube is three-dimensional.” [3]
Where did the idiots of Mathematics ever get such a stupid idea that they could have easily 'proven' to be
false? The number of numbers has absolutely nothing to do with why a rectangle is 2-D and a cube 3-D.
Let’s 'prove' it to them…
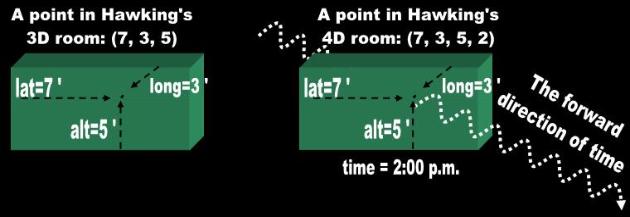
Hawking will certainly not object if we depict his quantitative example with the ordered triplet (7, 3, 5), where
latitude=7, longitude=3 and altitude=5. Thus, following his line of reasoning to its logical conclusions, we
arrive at the next level. Hawking asserts that space-time is four-dimensional because he requires four
coordinates or numbers to pinpoint an event within our Universe:
- “ An event is something that happens at a particular point in space and at a particular
time. So one can specify it by four numbers or coordinates...one can use any three
well-defined coordinates and any measure of time. In relativity, there is no real
distinction between the space and time coordinates...It is often helpful to think of the
four coordinates of an event as specifying its position in a four-dimensional space
called space-time. It is impossible to imagine a four-dimensional space.” (p. 2x) [4]
Let's test Hawking's claims. Consistent with his instructions, let's assume that the point was inside the room
at the specified coordinates at 2:00 o'clock or after 2 hours (Fig. 1). We can depict this point or event with an
ordered quartet – for example (7, 3, 5, 2). According to Hawking, his room is no longer 3-D, but is now 4-D!
And if we add temperature and the fact that he was angry that day, it now is 6-D! Clearly, the mathematical
definition of dimension cannot be used consistently in a scientific dissertation.
As always, the mathematicians choose all of the above and in this manner ensures that he covered all the
bases. Predictably, this makes for fascinating circular conversations among them. For instance, Hawking
confuses structure with location:
- “ We must accept that time is not completely separate from and independent of space,
but is combined with it to form an object called space-time…one can describe the
position of a point in space by three numbers, or coordinates. For instance, one can
say that a point in a room is seven feet from one wall, three feet from another, and five
feet above the floor. Or one could specify that a point was at a certain latitude and
longitude and a certain height above sea level…” (p. 23) [5]
It is often helpful to think of the four coordinates of an event as specifying its position in a four-dimensional
space called space-time. It is impossible to imagine a four-dimensional space.” (p. 24)
Hawking is talking about two unrelated subjects in the same dissertation and invoking physical dimensions
(length, width, and height) in the context of location. In the first description, he is talking about locating a
point on an object (space-time):
- “ Even these coordinates would not be of much use in describing the position of the
sun in our galaxy or the position of our galaxy in the local group of galaxies. In fact,
one may describe the whole universe in terms of a collection of overlapping patches.
In each patch, one can use a different set of three coordinates to specify the position
of a point.” (p. 23) [6]
In the second explanation he invokes a fourth coordinate, but incongruously tells us that he cannot imagine
the resulting object. This fourth coordinate is time, which Hawking tells us is indistinguishable from the
spatial coordinates:
- “ In relativity, there is no real distinction between the space and time coordinates, just
as there is no real difference between any two space coordinates.” (p. 24) [7]
Hawking is inconsistent with his use of the words coordinate and dimension. Is his famous room 3-D or 4-D
(Fig. 1)?
We see here that the mathematician’s room is three-dimensional with or without time. The addition of time
in his description did not alter the dimensionality of his universe. An expanding sphere remains a 3-D solid
throughout the experiment. A balloon does not convert into a 4-D object simply because you inflate it. And
if we added that the temperature in the room is 40 degrees or that the point has a mass of 40 kilograms, it
would not affect our result either.
It is the ridiculous definition of dimension of Mathematics that leads to inconsistent conclusions. For
example, what does the fact that Hawking includes time (or temperature or mass) have to do with his
inability to visualize his alleged 4-D object? If we use longitude, latitude, and altitude to locate a chair
within his room, we can see the room and the chair. If we now specify that the chair was located there at
2:00 o’clock, we can still visualize the room and the chair. Visualization has nothing to do with coordinates
and locating objects. It has solely to do with those structural aspects that mathematicians call intuitive and
philosophical. When Hawking says that he cannot visualize a 4-D object he is invoking not the mathematical
definition of dimension (longitude, latitude, altitude, and a hypothetical coordinate perpendicular to all three),
but rather the physical definition (length, width, height, and a hypothetical coordinate perpendicular to all
three). Hawking has inadvertently switched to the physical definitions. If Hawking doesn’t understand the
difference between a coordinate, a vector, and a dimension, then what can you expect of the remaining
mathematicians of the world?


| A sea urchin is a multidimensional being. Its rays stick out in every direction. |
Fig. 1 Mathematical Dimensions Quiz: Is Hawking's room 3-D or 4-D |
Relativists may argue that the point in Hawking's room is not moving and, therefore, time is undefined or
equal to zero. According to their own definition, a point is just a pictorial representation of a static location.
So, there is no contradiction between Fig. 1 and the relativistic definition of the event point.
So let's make the argument hermetical. Let's now put two boxers in the room and have them engage in a
2-hour bout starting at 2:00 o'clock. Will the room now be 4-D? Did factoring time or motion into this 'event'
change the shape or the dimensions of Hawking's room? Does the room become 10-dimensional because
one boxer threw 10 punches and each punch requires a different set of coordinates? Relativists forget that
they defined an event as 'a point in space-time.' [10] Any way they wish to view it, time involves two or more
locations. Therefore, it makes no sense to depict an event with a dot.
This argument confirms that the much heralded relativistic sphere is after all not an analogy, but rather a
mockup of space-time! Whether it is conceived as a static object or as one inflating 'through' time the sphere
never changes its three physical dimensions: length, width and height. The point of this example is to
underscore that we reach different conclusions regarding the dimensionality of the room if we use the
mathematical instead of the physical definitions of dimension. For the purposes of Physics, the room always
remains 3-D whether we factor the relativistic dimensions of heat, mass, size, time, exponent, or love.
And this raises suspicions about Hawking's declared inability to imagine his '4-D' space which, as it turned
out, was all along nothing other than our everyday '3-D space'. If Hawking intends to use the term 'four-
dimensional' to designate space-time under the pretext that he is talking about the number of numbers
needed to locate a point within the Universe, he should at least realize that he is using it out of context to
refer subsequently to the qualitative orientations of space-time. But then, when he confesses his inability to
visualize his 4-D space – a physical four-dimensional object – we are at a loss to understand what he was
talking about in the first place. Was he in retrospect referring to the ordered quartet of Mathematics or to the
traditional dimensions of Physics?
Perhaps some of the foregoing statements give us a clue. For instance, in his 2-D example, Hawking uses
the words latitude and longitude when he is actually talking about parallels and meridians. Obviously
relativists don't understand the difference between coordinates and number lines. Coordinates belong
exclusively to Physics; parallels and meridians belong exclusively to Math. Then, in his qualitative 3-D
example, Hawking pairs height (a dimension) with latitude and longitude (two of the coordinates). This
shows that relativists don't understand the difference between a dimension and a coordinate either. How is
it possible for professional theorists to make such elementary errors? Doesn't Hawking realize that height is
a different animal than altitude? If relativists rely on qualitative epithets of Physics to designate their ordered
'numbers', they should at least get them straight when they flaunt their vast knowledge in popularizations.
These are not trivial errors, nor are they oversights or typos. Relativists consistently confuse the
mathematical with the physical versions of dimensions in just about every paragraph they write. Evidence
of this is the dichotomy topologists and geometers live with today. Topologists erect their complex figures
gradually using simpler building blocks. The more faces an object has, the more coordinates or numbers
needed to locate a point on a given face, and the more dimensions it supposedly has. For mysterious
reasons, relativists forbid the coordinates to 'run' through the interior of the hollow 'solid'. They absolutely
demand that you hold the course and cross boundaries on its surface. [11] This requirement violates the
notion of dimension of Physics – length, width, and height – which conceptually extend through objects.
Thus, the topologist regards a multi-faced object called an icosidodecahedron to be 32-dimensional when,
for the purposes of Physics, it is just another 3-D geometric figure. Not a single simplex the topologists can
imagine surpasses 3-D. When Hawking explains that space-time is 4-D because we can specify a point
within it with 4 numbers or coordinates, he invokes the topological notion used by mathematicians. But when
Hawking confesses that he cannot visualize a four-dimensional object, he has unwittingly reverted to the
qualitative definition used in Physics (length, width, and height). This is how mathematicians go back and
forth and get confused with their inconsistent definitions. This is how they end up drawing a 3-D solid and
calling it a 4-D object. This is why, despite declaring space-time to be 4-D, our mathematicians unanimously
depict this object with a 3-D sphere and say they cannot imagine it. If throughout all these years relativists
have been relying on the topological definition of dimension to describe space-time, they have now run out
of excuses for their refusal to pull out their crayons!
Of course, with such versatile definitions and usages, it is not surprising that relativity can explain everything
and anything. Relativity has become an unfalsifiable theory simply because the alleged object space-time in
which we live is constructed with every possible meaning of the word dimension. The dimension of relativity
is static and dynamic, and includes length, width, height, longitude, latitude, altitude, depth, breadth, and
elevation:
- “ the physical space as we understand it has three independent "degrees of freedom,"
or three directions in which we and the other objects in space are able to exist, expand,
or move. For example: length, width, height; latitude, longitude, altitude; Elm street,
fourth building down, second floor; x, y, z.” [12]
[Okay. So a degree of freedom is something that has direction I got it!]
“ Now, the idea of the fourth dimension (or the idea of the first four dimensions all
together) is an idea we use to describe any quality, state, object, event, or concept
which requires four independent degrees of freedom (ways in which it is able to be
different) in order to describe it completely. For example: length, width, height, weight;
latitude, longitude, altitude, temperature; Elm street, fourth building down, second floor,
9 O'clock on Thursday; x,y,z,w. It's really that simple. [13]
[Huh? How did temperature make the list? Answer: The mathematician redefined the
crucial term ‘degree of freedom.’ A degree of freedom is no longer a direction, but a
way in which something is different. He borrowed a dimension from the ‘Physics’ list.
He is no longer talking about direction.]
“ The only reason people get confused about it is because they cannot visualize it. If I
tell you the length, width and height of an object, you can get an idea of what it looks
like, perhaps a cube or a long slender rod or anything in between. But if I also tell you
what temperature something is or how much it weighs, what does that look like?” [14]
[The object should look exactly the same! Its dimensions continue to be length, width,
and height. If you don’t believe me, do the experiment in your lab, and verify my claim!
Take a cube and heat it. It should still have length, width, and height, the three dimen-
sions! If not, it is by definition NOT a cube!
The mathematician succeeds with this argument only after redefining the term
'degree of freedom' from ‘that which has direction’ to ‘that which is different.’
By the way, temperature does not have direction, and this explains why it is not a
dimension. Neither is time nor mass.]
“ The problem with visualization becomes even more acute when we try to graph the
data. You can make a drawing of a three-dimensional object on a flat piece of paper,
and you can even make a model to represent three-space, like a relief map that shows
the elevation of the ground at every point over a given area. But when you try to draw
a picture of four-dimensional space it is impossible.” [15]
[ The mathematician is saying that we can ‘get an idea what an object that has length,
width, and height looks like,’ but that we cannot ‘draw a picture of an object that has
length, width, height, plus an alleged 4th dimension running perpendicular to all three.
This fourth dimension is allegedly like the other dimensions, a straight line perpendicular
to the other three and quite unlike ‘temperature.’ Pursuant to the mathematical definition
of dimension, temperature is not a dimension. The dimension of Mathematics is a coor-
dinate. Therefore, the mathematician invokes irrelevant ‘dimensions’ such as temperature
and weight to justify why you can’t visualize a 4-D object when they have nothing to do
with the subject at hand. The fact that we cannot visualize temperature or weight has
nothing to do with dimensions.]
- The mathematicians do this over and over again. In Mathematics, they call a coordinate a dimension and
never realized that there is a difference. Then they invoke and mix with these the dimensions of ‘Physics’, –
mass, time, temperature, love, peace, beauty – which have nothing to do with coordinates or with dimensions.
Thus the mathematician concludes that there are ‘infinite’ dimensions because anything can be a dimension.
That’s why they can’t answer your question. There are simply too many variables and we don’t know them all.
The misconceived definition of dimension of Mathematics is unacceptable in science because it leads to
ridiculous conclusions. If we can think of 500 dimensions, is an object 500 D? What meaning can it have to say
that an object is 500-D?
Clearly a cube is not 3-D because of the number of coordinates needed to locate a point on its surface. A cube
is 3-D because, like all solids, this object faces in three mutually-orthogonal directions. This is the only context
in which we can use the word dimension consistently in Science.
| Hawking's 4D room: “It is often helpful to think of the four coordinates of an event as specifying its position in a four- dimensional space called space-time… In relativity, there is no real distinction between the space and time coordinates... It is impossible to imagine a four-dimen- sional space.” (p. 24) [9] |
| Hawking's 3D room: “...one can Describe the position of a point In space by three numbers, or coordinates. One can say that a point in a room is seven feet from one wall, three feet from another and five feet above the floor.” (p. 23) [8] |

| Bill is truly a multi-dimensional individual! He has vectors and coordinates sticking out in every direction. |

- Module home page: The mathematical definition of dimension is unscientific
- Pages in this module:
- 4. This page: The multi-dimensional 'number of numbers' definition of Math is unscientific

- ________________________________________________________________________________________
- Copyright © by Nila Gaede 2008
